271 words
1 minutes
多獨立變數求解速度分布
TIP
- 推爆信龍的影片,真的有夠會教,會聽到熱血沸騰那種XD
- 熟悉PDE解法,因為工數這部份講到的不多
- 考試心得:應用題的話切記注意單位換算 (質均)!
- TP Resources (Notes更新中)
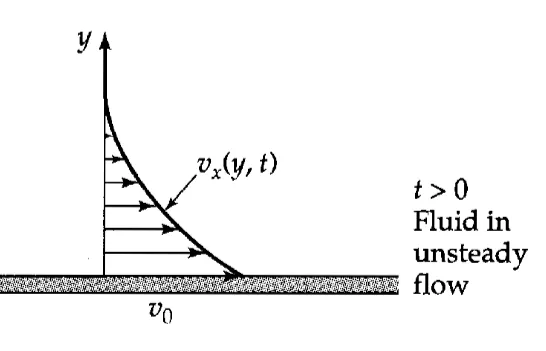
Time-Dependent (Unsteady-state) Flow
Assumptions of the System
- Newtonian Fluid
- Incompressible (constant density)
- 1D Laminar Flow (Re < 2100)
Solve for Velocity Distributions
用CH3學到的通用 “equations of change (continuity & motion)” 求解速度分布:
- 平面上無限延伸的流體
- 無因次變數的假設技巧 (詳情見筆記)
- 因B.C.非有限範圍,此PDE不能用最方便的分離變數法,改用 “combination of variables” (較不直覺)
- 管子內的流體 (flow between 2 plates)
- B.C.為有限範圍,PDE可用分離變數法求解,但是需先用 “perturbation” 把變數 都搞成0
- 接著就是:分離變數 (PDE to ODE) -> 典型 S-L 問題,記得考慮eigenvalue的三種情形 -> 代回I.C.和B.C.,展開傅立葉級數得到近似解 (因用perturbation作前提假設)
Stream Function
Creeping flow around a sphere
Boundary-Layer Theory
Assumptions of the System
- Newtonian Fluid
- Incompressible (constant density)
- 2D Laminar Flow (Re < 2100)